OPTIMIZATION AND RELIABILITY OF BUILDING SYSTEMS
JOURNAL: CONSTRUCTION ECONOMIC AND ENVIRONMENTAL MANAGEMENT Volume №2 (79), 2021
Section 4. Problems of construction organization
Publication text (PDF): Download
UDK: 620.004.5; 35.073.5
AUTHOR AND PUBLICATION INFORMATION
AUTHORS:
- Chemodurov V.T., V.I. Vernadsky Crimean Federal University, Simferopol, Crimea
- Litvinova E.V., V.I. Vernadsky Crimean Federal University, Simferopol, Crimea
TYPE: Article
DOI: https://doi.org/10.37279/2519-4453-2021-2-110-117
PAGES: from 110 to 117
STATUS: Published
LANGUAGE: Russian
KEYWORDS: reliability, optimization, failure, random character of quantities, simulation simulation.
ABSTRACT (ENGLISH): A new method for optimizing construction systems is proposed while taking into account the given level of reliability of their functioning. Proposed method is effective for problems in which the vector of optimal parameters of a building system belongs to one or more functional constraints. In practice, such tasks constitute a substantial majority. The main advantage of this method is that the construction costs for the production of the building system or its elements are minimal.
ВВЕДЕНИЕ
Надежность любой конструкции является по существу конструктивным параметром, который должен вводиться в систему на этапе проектирования. При проектировании любой конструктивной системы следует иметь в виду, что ее рабочие характеристики и параметры являются вероятностными по своей природе. Очевидно, что факторы, определяющие прочность элементов и действующие на них нагрузки, также являются вероятностными. Это означает, что при оценке показателей надежности на этапе проектирования необходимо учитывать вероятностный характер параметров системы.
В данной статье рассматривается подход к проектированию конструкции при заданных характеристиках надежности ее элементов. Однако характеристики конструктивной системы после ее создания могут ухудшаться постепенно с течением времени. Иногда только тонкая грань отделяет исправное состояние системы от отказа. Учет изменения характеристик надежности системы в период ее эксплуатации, а также восстановление надежности, являются теми вопросами, которые являются темами будущих исследований. На степень сохранения заданных уровней надежности системы влияет объем профилактического технического обслуживания. И если вопросы технического обеспечения уровней надежности системы предусматриваются, то они также входят в оценку надежности при ее проектировании.
Итак, уровень надежности системы должен устанавливается при ее проектировании, а реализуется данный уровень уже во время эксплуатации, то есть проявляется способность объекта выполнять свои функции в течение установленного срока службы. Реализация состояния объекта, при котором он не сможет выполнять свои функции, называется отказом.
На современном этапе развития науки проектирование любых конструктивных систем строится путем решения двух противоречивых задач. С одной стороны, система должна обладать высоким уровнем надежности, что требует дополнительных материальных затрат. С другой – обладать высокой экономичностью. Обе задачи вполне возможно объединить в одну, используя законы и методы системного анализа.
АНАЛИЗ ПУБЛИКАЦИЙ, МАТЕРИАЛОВ И МЕТОДОВ
Традиционные методы расчета конструкций основаны на предположении о полной определенности в таких параметрах, как внешняя нагрузка, свойства материалов, геометрические размеры и форма проектируемого изделия [1]. Между тем, как было сказано выше, все эти факторы находятся под влиянием большого количества разнообразных причин, и поэтому в той или иной мере носит изменчивый характер. Так, все внешние нагрузки и механические характеристики материалов являются случайными. В меньшей мере проявляется изменчивость геометрических размеров и форм элементов конструкций. Случайных характер основных расчетных величин при традиционном методе расчета прочности сооружений учитывается при выборе коэффициентов безопасности [1]. Однако дать однозначный ответ на объективность данного коэффициента довольно затруднительно. Его величина, как правило, зависит от большого числа испытаний, либо обработки статистического материала при реализации математических моделей отказа отдельных узлов. Наконец, путем экспертных оценок устанавливается его величина и вводится в руководящий документ.
До 90–х годов XX века действовали правила метода допускаемых напряжений, при котором основным требованием выполнялось следующее неравенство для любого волокна конструкции [2]
![]()
Здесь: ![]() − допускаемое напряжение;
− допускаемое напряжение; ![]() − напряжение в волокне, определяемое методами строительной механики; n − коэффициент запаса.
− напряжение в волокне, определяемое методами строительной механики; n − коэффициент запаса.
При таком методе проектирования работа строительных конструкций рассматривалась в упругой стадии деформаций, и не учитывались пластические свойства материалов. Также коэффициент запаса для всех конструкций из данного материала был одинаков, что не отвечало фактической работе комплексных материалов (железобетона и каменной кладке). В них бетон и арматура, кирпич и раствор имеют различные механические характеристики, поэтому с различной быстротой исчерпывают свою несущую способность.
Для учета работы материалов в области пластических деформаций перешли к методу проектирования по разрушающим нагрузкам [3-5]. Данный метод стал использоваться для железобетонных конструкций с 1938 г., а для каменных с 1943 г. Данный метод требует выполнение следующего неравенства
![]()
Здесь: Fн − нормированное значение нагрузки; Rн − нормативное значение несущей способности (гарантированной прочности); − коэффициент запаса.
Нормирование параметров расчета строительных конструкций получили дальнейшее развитие в методе предельных состояний [6-8]. Данный метод включен в строительные нормы и правила [2].
Введение метода предельных состояний позволило учесть специфику работы конструкций, фактическую изменчивость нагрузок и несущей способности. Использование данного метода предполагает наличие статистических данных по нагрузкам, механическим свойствам материалов и условий работы конструкции. Также в данном методе предусматривается учет выхода конструкции из строя. Здесь вводится понятие «обеспеченности» расчетных значений: для нагрузки – вероятность того, что она окажется меньше расчетного значения; для прочности конструкции – вероятность того, что она будет больше расчетного значения.
ЦЕЛЬ И ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЙ
Обоснование оптимальных решений для определения надёжности строительных систем на основе критериев надежности, численные значения которых называются показателями (количественные или статистико-вероятностные характеристики) надежности. Сама же надежность объекта зависит от условий эксплуатации.
Основная задача – рассмотреть количественные характеристики, позволяющие сравнивать строительные системы по надежности, оценивать срок их службы, необходимое количество, частоту профилактических осмотров и ремонтов и т.п.
ОСНОВНОЙ РАЗДЕЛ
Формирование уровня надежности строительной конструкции происходит в процессе ее проектирования, изготовления и возведения. Во время эксплуатации конструкции этот уровень надежности реализуется. При этом проявляется способность объекта выполнять свои функции в течение установленного срока службы, которая называется надежностью. Реализация состояния объекта, при котором он не сможет выполнять свои функции, называется отказом.
Мерой надежности является вероятность безотказной работы за заданный срок службы. Вероятностный подход к оценке надежности обусловлен тем, что внешние и внутренние воздействия на конструкцию, физические и геометрические характеристики элементов самой конструкции представляют собой случайные величины или случайные процессы.
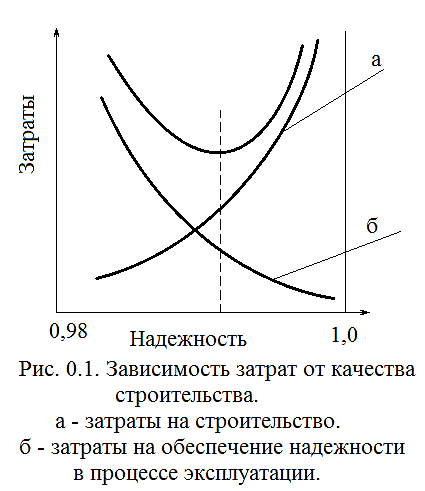
Рис. 1. Зависимость затрат от качества строительства:
а – затраты на строительство;
б – затраты на обеспечение надёжности в процессе эксплуатации.
При проектировании строительных систем необходимо разрешить противоречие, которое связывает стоимость и эффективность конструкции. Эффективность строительной системы тем выше, чем выше уровень ее надежности, что соответствует длительной ее эксплуатации без особых текущих затрат. С другой стороны, соответствующий уровень надежности достигается за счет различных затрат на ее создание. Таким образом, увеличение материальных затрат на создание строительной системы снижает расходы на ее эксплуатацию. Снижение надежности приводит к отказам строительной системы и росту расходов на ее восстановление в процессе эксплуатации. Разумное удовлетворение данных противоречий приводит к принятию «целесообразного» уровня надежности конструкции. Данный «целесообразный» уровень надежности при предварительных исследованиях можно определить графическим путем, как показано на рис. 1.
При создании любого строительного сооружения необходимо обеспечить разработчика достаточным уровнем информации для обоснования решений. В зависимости от инструмента, с помощью которого получают нужную информацию, исследования делятся на теоретические и экспериментальные. Этим инструментом являются методы физического и математического моделирования. Сочетание теоретических и экспериментальных исследований, то есть физического и математического моделирования, позволяет наиболее рационально использовать априорную информацию (предыдущий опыт) и оперативную (текущую) информацию о выполнении принятых решений в качестве основы для принятия следующих решений.
Задача о показателях надежности, которые могут быть использованы при формировании требований к строительным конструкциям значительно сложнее. Такую задачу достаточно просто решить для какого-либо узла конструктивной системы. В действующих нормах основное расчетное требование для строительных конструкций формулируется в виде неравенства
![]()
Здесь Rp и Fp − расчетные значения несущей способности и нагрузочного эффекта.
В работе [9] предлагается оценивать вероятность отказа как вероятность реализации неравенства (1). Пусть – плотность распределения Тогда вероятность не разрушения конструкции в данном расчетном случае
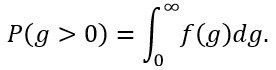
Выражение (2) позволит дать разовую оценку вероятности отказа, например при проектировании. В теории надежности термин «отказ» означает, что система прерывает способность выполнить требуемые функции по прошествии какого–либо времени, то есть является функцией времени [10-11]
![]() (3)
(3)
Здесь Т – случайная величина, обозначающая наработку до отказа; Q(t) – функция распределения наработки до отказа.
Вероятность безотказной работы или вероятность того, что невосстанавливаемая система будет выполнять требуемую функцию в заданный момент времени t, можно записать в виде
![]() (4)
(4)
Задачи (2) и (4) довольно легко решаются, если известны функции распределения несущей способности системы и нагрузки.
Обе задачи имеют большое значение при проектировании строительных конструкций. Важность задачи (4) заключается в том, что она позволяет устанавливать сроки восстановления назначенных функциональных способностей систем. Кроме того, позволяет организовать систему технического обеспечения системы с целью поддержания ее на заданном уровне работоспособности. Исходными данными для расчета отдельных узлов строительной системы являются:
- функции распределения несущей способности и нагрузочного эффекта;
- среднее время наработки на отказ;
- интенсивность отказов.
Все перечисленные исходные данные определяются на основе сбора и обработки статистических данных опыта эксплуатации однородных элементов.
Теперь обратимся к строительной системе в целом, состоящей из большого (если не сказать огромного) количества отдельных элементов.
На сегодняшний день существует несколько подходов к оценке надежности системы в целом. Один из них связан с поиском «горячих точек», то есть наиболее уязвимых элементов системы [9]. Другой метод связан с имитационным моделированием расчета надежности системы [10-11].
И в том и в другом случаях необходима кропотливая работа в процессе разработки имитационных моделей системы, состоящей из последовательно или параллельно соединенных блоков (элементов), которые имитируют реальную конструкцию.
Анализ надежности систем с помощью имитационных моделей представляет собой определенную форму предварительного анализа. Он используется для оценки возможного состава элементов на этапе проектирования и определения необходимых уровней надежности подсистем и элементов. По мере перехода проектирования на заключительные этапы может выполняться более детальный анализ.
Авторами предлагается способ оптимизации параметров строительной системы или ее элементов, учитывающий заданную вероятность их функционирования. То есть, предполагается решать одновременно две задачи и оптимизации параметров строительной конструкции и обеспечение заданного уровня ее надежности. Предполагается, что такой подход позволит создавать объекты со значительной экономией материальных ресурсов.
Общая постановка задачи линейного программирования имеет вид: найти минимум целевой функции (рис. 2)
![]()
при выполнении условий по функциональным ограничениям
![]()
и ограничениям по параметрам
![]()
После определения оптимального решения в детерминированной постановке необходимо определить параметры распределения функциональных ограничений в области данного оптимального решения.
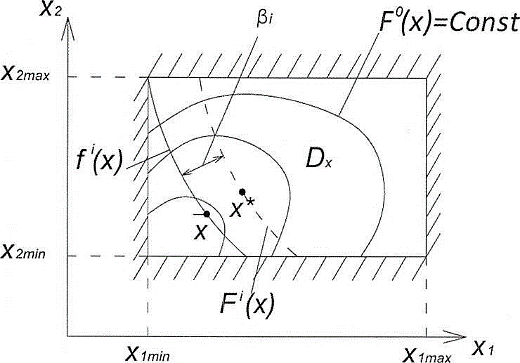
Рис. 2. Поиск оптимума в задачах с ограничениями по вероятности
Необходимо отметить, что случайные переменные, которые в сложных системах представляют наложение многих различных более или менее независимых причин, могут рассматриваться как сумма случайных переменных. Известно, что сумма произвольного распределенных случайных переменных приближенно распределена по нормальному закону, причем тем ближе, чем больше членов этой суммы (центральная предельная теорема). Это служит основой того, что многие статистические распределения при достаточном объеме выборки хорошо аппроксимируются нормальным распределением.
На втором этапе оптимизации необходимо уточнить функциональные ограничения (7), то есть назначить новые границы оптимизационной задачи с заданной вероятностью их не нарушения. В этом случае необходимо провести статистический анализ ограничений (7), используя данные по статистическому разбросу характеристик прочности и нагружения. В новой постановке ограничения (7) примут вид
![]()
В этой формуле
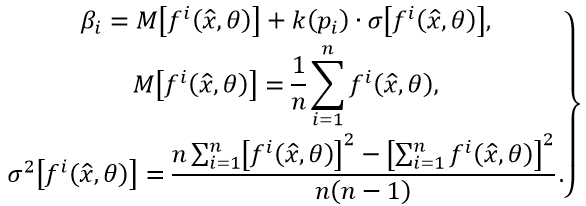
Здесь: ![]() − квантиль нормированного нормального закона распределения, соответствующая заданной вероятности − вектор случайных параметров, входящих в задачу проектирования pi;
− квантиль нормированного нормального закона распределения, соответствующая заданной вероятности − вектор случайных параметров, входящих в задачу проектирования pi; ![]() − объем выборки.
− объем выборки.
На рисунке 2 показана геометрическая интерпретация описанного метода для двух варьируемых параметров.
РЕЗУЛЬТАТЫ И ИХ АНАЛИЗ
Вопросы надежности элементов и систем в общей постановке изложены выше. Однако, учитывая структурную сложность элементов строительных конструкций и особенности их эксплуатации, для расчета надежности и эффективности сооружений требуются более подробные сведения о характеристиках надежности. Кроме того, существенным является сохранение численных значений показателей надежности сооружений, полученных при проектировании и возведении объектов. Эта задача должна возлагаться на систему обеспечения строительных сооружений.
Для анализа надежности систем сооружений все параметры, определяющие состояние конструкции в части надежности, целесообразно разделить на следующие три группы:
− неконтролируемые, неизменяющиеся во времени параметры; надежность по этим параметрам обозначим Pнкн
− неконтролируемые, изменяющиеся во времени параметры; надежность этих элементов определяется так
![]()
где ![]() − интенсивность отказов по неконтролируемым параметрам;
− интенсивность отказов по неконтролируемым параметрам;
− контролируемые, изменяющиеся во времени параметры; надежность по этим параметрам представим так
![]()
где ![]() − интенсивность отказов по контролируемым параметрам.
− интенсивность отказов по контролируемым параметрам.
Надежность за счет параметров первой группы является обычно следствием производственных просчетов в ходе изготовления элементов систем и их монтажа и неподвергающихся контролю (технологические формы узлов, элементов, нарушения и ошибки монтажа, установка неработоспособных непроверяемых в ходе эксплуатации деталей и тому подобное).
Наличие двух других групп параметров определяется практической невозможностью осуществить глобальный контроль, то есть охватить контролем все без исключения элементы, влияющие на надежность системы.
Процесс изменения уровня надежности во времени с учетом условий реальной эксплуатации наглядно иллюстрируются графиками (рис. 3), которые можно было бы принять в качестве модели надежности элементов строительных сооружений. Как видно из графиков, функция надежности имеет сложную структуру. Эксплуатация элементов строительных конструкций может быть представлена в виде ряда состояний, которые сменяют друг друга и отличаются в основном интенсивностью отказов. На рисунке 3 условно показаны два характерных участка процесса эксплуатации: tэ − режим эксплуатации; tп − режим проверки системы на функционирование, характеризующийся повышенной интенсивностью отказов.
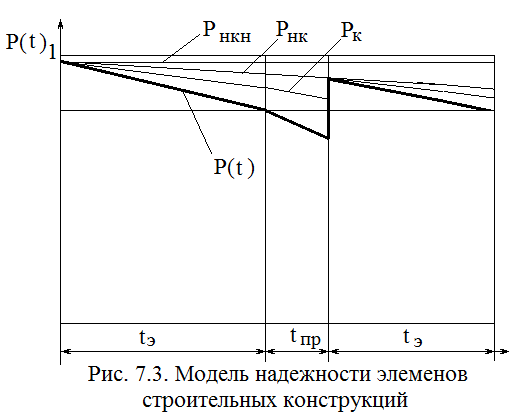
Рис. 3. Модель надёжности элементов строительных конструкций
Предполагая отказы по группам параметров независимыми, функция надежности для системы в целом P(t) может быть представлена следующими выражениями:
![]()
− с начала эксплуатации до контроля
− после контроля для систем, оставшихся исправными,
![]()
где tпп − время последней проверки.
Из приведенных графиков можно сделать следующие два важных вывода.
- Любая лишняя проверка на функционирование наносит потенциальный ущерб системе в смысле надежности из-за повышения интенсивности отказов при проверках по неконтролируемым параметрам.
- Для невосстанавливаемых систем, если не предполагается замена неисправных элементов на новые исправные, проверки на функционирование не выгодны, так как это снижает долю исправных систем из-за повышенной интенсивности отказов при проверках и по контролируемым параметрам.
- Имея графики снижения надежности во времени строительной системы в целом, либо ее подсистем имеется возможность осуществлять планирование мероприятий по всем видам обследований и восстановительных работ с целью поддержания системы в работоспособном состоянии. Данные сроки проверки и восстановления, естественно, будут зависеть от заданного уровня вероятности безотказной работы системы и ее подсистем.
Количественный вклад контролируемых и неконтролируемых параметров в функцию надежности системы принято оценивать глубиной контроля ![]() , определяемой выражением
, определяемой выражением
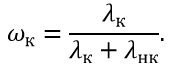
Динамические модели являются естественным обобщением статических моделей. Для использования динамических моделей необходимо для каждой системы знать распределения наработки до отказа, а это означает, что требуется достаточно большой объем данных об отказах систем. Часто при использовании динамических моделей удобно принимать допущение о постоянной интенсивности отказов. Принятие этого допущения целесообразно в том случае, когда система при анализе не разбивается на слишком большое число мелких подсистем, так как крупные подсистемы, состоящие из многих элементов, во время эксплуатации имеют практически постоянную интенсивность отказов.
Такие свойства системы, как эксплуатационная готовность, удобство обслуживания, ремонтопригодность являются важными для анализа общей эффективности функционирования системы. Показатели, характеризующие эти свойства, зависят также от факторов, которые являются внешними по отношению к системе, например таких, как наличие запасных элементов, доступность средств ремонта, легкость ремонта.
ВЫВОДЫ
- Традиционные методы учета надежности конструктивных систем связаны с наличием достаточно большой базой данных по параметрам, имеющих случайную природу, или проведения многочисленных экспериментов. Кроме того необходимо доказывать те или иные виды распределений как прочности изделий, так и напряжений в них, которые возникают при нагрузках случайной природы.
- Предлагаемый авторами метод конструирования строительных систем сочетает задачу оптимизации элементов конструкции и учет задания вероятности их функционирования в течение заданного времени.
При этом задача оптимизации решается в три этапа.
На первом этапе решается задача оптимизации параметров строительной системы в детерминированной постановке методами нелинейного программирования. При этом, одновременно, минимизируются материальные затраты на создание конструкций.
На втором этапе исследуется стохастическая модель системы с учетом случайного разброса параметров, имевших случайную природу. На этом этапе определяются параметры случайных функциональных ограничений в области оптимизированного решения, полученного на первом этапе, и формулируются новые функциональные ограничения, обеспечивающие заданную надежность конструкции.
На третьем этапе вновь в детерминированной постановке решается оптимизационная задача, но уже при новых ограничениях. Полученные при этом повышенные материальные затраты на создание конструкции в любом случае будут минимальны.
- С целью поддержания строительных сооружений на высоком уровне надежности и долговечности необходимо совершенствовать систему технического обеспечения, для чего развивать как статическую, так и динамическую методики паспортизации объектов.
- Материальные затраты на проектирование и возведение объектов, с одной стороны, и на их эксплуатацию, с другой должны быть глубоко обоснованы. Это обоснование представляется так же оптимизационной задачей и является методом исследования еще на этапе проектирования строительных сооружений.
ЛИТЕРАТУРА
- СП 63.13330.2012. Бетонные и железобетонные конструкции. Актуализированная редакция СНиП 52– 01–2003. – М. Минстрой России. – 2015. – 162 с.
- ГОСТ 27751–2014. Надежность строительных конструкций и оснований. Основные положения. – М.: Минстрой России, 2014. – 26 с.
- Ушаков, Игорь. ЖИВА ЛИ ЕЩЕ ТЕОРИЯ НАДЕЖНОСТИ? – Session Reliability in Applications. – С. 188–199. [Электронный ресурс]. – Режим доступа: https://www.tsi.lv/sites/default/files/editor/ science/Publikacii/RelStat_06/ed_session4_06.pdf.
- Третьяков, А.М. Основы теории надежности: учебное пособие / А.М. Третьяков; Алт. гос. техн. ун-т, БТИ. – Бийск: Изд-во Алт. гос. техн. ун-та, 2016. – 106 с.
- Гнеденко, Б.В. Вопросы математической теории надежности / Б.В. Гнеденко [и др.]. – Москва: Радио и связь, 1983. – 376 с.
- Голинкевич, Т.А. Прикладная теория надежности / Т.А. Голинкевич. – М.: «Высшая школа», 1985. – 16 с.
- Острейковский, В.А. Теория надежности: учебник для вузов / В.А. Острейковский. – М.: Высшая школа, 2003. – 463 с.
- Половко, А.М. Основы теории надежности, 2-е издание / А.М. Половко, С.В. Гуров. – СПб.: БХВ-Петербург, 2006. – 702 с.
- Райзер, В.Д. Теория надежности сооружений. Научное издание. – М.: Издательство АСВ, 2010. – 384 с.
- Чемодуров, В.Т. Методы статистического оценивания в строительстве: учебное пособие / В.Т. Чемодуров, Э.В. Литвинова. – Симферополь: КФУ им. В.И. Вернадского, 2015. – 156 с.
- Чемодуров, В.Т. Моделирование систем: монография / В.Т. Чемодуров, Э.В. Литвинова. – Симферополь: ИТ «АРИАЛ», 2016. – 236 с.
