BENDING OF AN INFINITE BEAM ON A BASE WITH TWO PARAMETERS IN THE ABSENCE OF A PART OF THE BASE

JOURNAL: CONSTRUCTION ECONOMIC AND ENVIRONMENTAL MANAGEMENT  Volume №2 (79), 2021

Section 4. Problems of construction organization

Publication text (PDF): Download

UDK: 624.072

AUTHOR AND PUBLICATION INFORMATION

AUTHORS:

1. Aleksandrovskiy M.V.
2. Rybin E.N.

TYPE: Article

DOI:

PAGES: from 118 to 127

STATUS: Published

LANGUAGE: Russia

KEYWORDS: absent of part the base with two parameters, infinite beam, method of generalized solutions, integral Fourier transform, integral equations, coefficient taking into account soil adhesion, analysis of the influence of a parameter that takes into account the distribution properties of the foundation.

ABSTRACT (ENGLISH): At this time, in connection with the high rates of development of construction and the improvement of calculation models, dealing into account the compatibility of the work of the base and the structures located on them, issues related to the use of various calculation methods become relevant. In the article, an effective analytical solution is built, obtained using the method of generalized solutions for bending a beam of infinite length, interacting with a two-parameter base, provided that there is no part of the base under the beam. The model in question is able to effectively take into account the distribution properties of the base by varying the coefficient reflecting the shear parameter, and also contains conditions that under some part of the beam do not have a base. By using integral transformations of the Fourier type, the original differential equation is reduced to a Fredholm integral equation of the second kind with a degenerate kernel, while all integrals are solved in analytical form and in explicit form, which leads to an increase in the accuracy of calculations in comparison with approximate methods. In this article the authors considered of solution of the problem of beam loaded with concentrated force applied at the origin at fixed length of the section with no base. The analysis of the change in the values of the calculated characteristics obtained for various numerical values of the parameter that takes into account the adhesion of the base is presented.

ВВЕДЕНИЕ

Современное проектирование и строительство зданий и сооружений немыслимо без четкого и ясного понимания особенностей их работы, и в частности, тех конструктивных элементов, которые взаимодействуют с основаниями. Уникальность возводимых объектов требует совершенствования методов расчета, при этом актуальными становятся вопросы, связанные с уточнением и совершенствованием параметров расчетных схем, отражающих взаимодействие сооружений и основания, а также и учет многочисленных факторов эксплуатационного, технологического и конструктивного характера. Значительная часть расчетов проектируемых сооружений связана именно с определением усилий в элементах, взаимодействующих с основанием. Строгость аналитических методов способна более детально и точно охарактеризовать поведение конструкций, что непосредственно способно отразится на их надежности и поэтому любое уточнение расчетов может существенно повлиять на стоимость, возводимого объекта. Такая постановка задачи в полной мере относится к ленточным фундаментам зданий и сооружений, промышленных и гражданских объектов, взлетно-посадочным полосам и дорожным покрытиям, условия эксплуатации которых, связаны с возможным проседанием основания и образованием пустот. Так, при проектировании ленточных фундаментов, расположенных на карстовых породах и просадочных грунтах в виде лессовых отложений, которые при замачивании дают большую осадку, следует учитывать возможность образования под фундаментами углублений, провалов и т.п. Отсутствие в расчетной схеме контакта балки с основанием может возникнуть на различных участках, в частности, в центре или вблизи края. При возникновении таких ситуаций возникает необходимость решения ряда самостоятельных задач при различных постановках граничных условий. Например, в том случае, когда нагрузка и провал грунта находятся под центральной частью ленточного фундамента, то его расчетную схему можно представить в виде бесконечной балки.

АНАЛИЗ ПУБЛИКАЦИЙ; МАТЕРИАЛОВ, МЕТОДОВ

Несмотря на разнообразие представленных в литературе расчетных моделей оснований и методик для их расчета эти методики обычно не связаны между собой и используются для решения частных задач.

Среди моделей упругого основания, использующих два параметра, можно отметить те, что были представлены в трудах М.М. Филоненко-Бородича П.Л. и Пастернака [2], а также В.З. Власова и Н.Н. Леонтьева [1]. Главным достоинством, двухпараметрических моделей явилась возможность учёта распределительной способности основания.

В дальнейшем, в статье при рассмотрении особенностей модели упругого основания будет использована трактовка, предложенная, В.З. Власовым и Н.Н. Леонтьевым [1], как «однослойного основания», характеризуемого двумя обобщенными параметрами. В такой модели упругого основания первый обобщенными параметрами (коэффициент) характеризует жесткость основания на сжатие, а второй – на сдвиг. Несмотря на различные идеи, предлагаемые для расчета балок на упругом основании, авторы приходят к одному тому же виду дифференциального уравнения

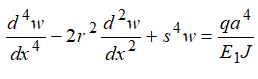(1)

где  r²и  s² — обобщенные упругие безразмерные величины, а˗ полудлина балки.

Несмотря на наличие различных методик для определения значений коэффициентов [3, 4, 5] в отчетах по инженерно-геологическим изысканиям, как правило, информация по упомянутым коэффициентам отсутствует. В SCAD Office в программе-сателлите ПАСТЕРНАК в качестве одной из возможных, используется методика, предложенная М.И. Горбуновым-Посадовым [6].

Как отмечалось выше, в рассматриваемой постановке задачи за основу принята модель, предложенная В.З. Власовым, Н.Н. Леонтьевым [1], а в качестве расчетных значений второго обобщенного параметра (коэффициента сдвига) согласно [7], принимаются значения:  k =0, k =0,5; и k =0,9.

Методика решения дифференциального уравнения вида (1) может рассматриваться как на основе строгих аналитических методов, например [7, 8, 9], так и с применением широко используемых, численных методов [10, 11].

В частности, для нахождения решения дифференциального уравнения, представленного в виде (1) может использоваться метод обобщенных решений, предложенный В.И. Травушем [9]. Представленный автором метод был применен для получения аналитического решения задачи изгиба бесконечной балки, расположенной на винклеровском упругом основании при отсутствии основания под частью балки [12]. Однако, главным недостатком у рассмотренной модели основания, явилось отсутствие возможности учета распределительной способности основания.

Общий вид решения дифференциального уравнения (1), с учетом условий отсутствия основания под частью балки, был представлен в работе [13] в форме уравнения (10). Однако, на наш взгляд, авторы ввели упрощение, обусловленное отсутствием сомножителя, определяемого функцией Хевисайда —  во втором слагаемом уравнения (10). Такое упрощение в случае реализации приведенного алгоритма должно было привести к занижению численных значений результатов расчета.

МАТЕРИАЛЫ И МЕТОДЫ      

Рассмотрим бесконечную балку, лежащую на упругом основании, описываемом моделью с двумя обобщенными параметрами (коэффициентами постели) [1], причем введем условия, учитывающие отсутствие основания под центральной частью балки на участке протяженностью (рис. 1.).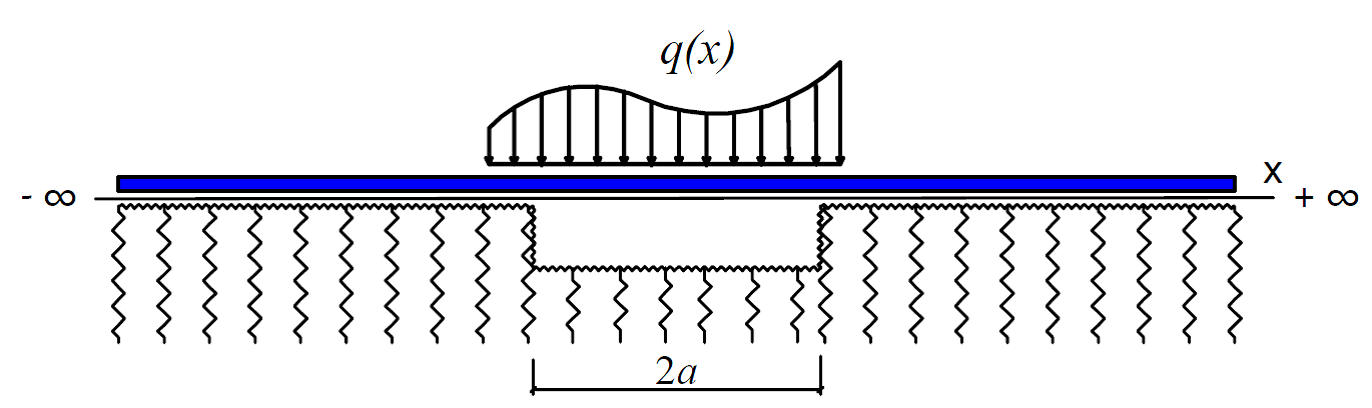

Рис.1. Схема бесконечной балки, лежащей на основании с двумя параметрами при отсутствии основания на заданном участке (разработано авторами)

В общем случае, действующая на балку, произвольно приложенная нагрузка, может быть представлена, как сумма симметричной и обратно симметричной составляющих.

Дифференциальное уравнение, описывающее прогиб балки при заданном условии в трактовке [1] примет вид

.

(2)

Уравнение (2) можно привести к безразмерным координатам, если ввести обычно используемую замену переменных:

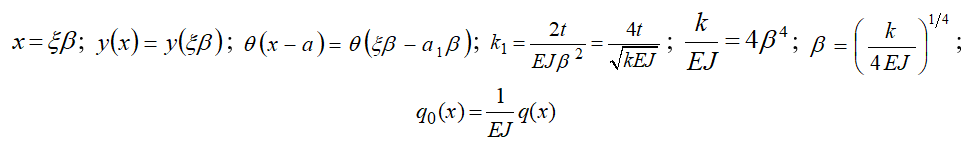(3)

Здесь E ˗ модуль упругости материала балки, J˗ ее момент инерции, t и k ˗ обобщенные параметры модели основания, k_j˗ второй коэффициент постели, а функция Хевисайда.

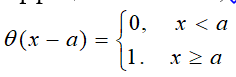
Дифференциальное уравнение изгиба относительно прогиба балки в безразмерных координатах и функциях с учетом (2) и (3) примет вид

.

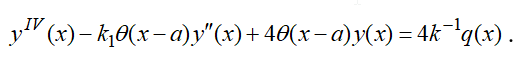(4)

Для решения уравнения (4) согласно [9] можно использовать преобразование Фурье для решения задач с бесконечной областью, когда функция y(x) и ее первые три производные не имеют разрывов в этой области.

Разложим произвольно действующую на балку нагрузку q(x) на симметричную и обратносимметричную. При действии симметричной составляющей нагрузки, применяя отдельно для каждого слагаемого уравнения (3) прямое косинус преобразования Фурье получим:

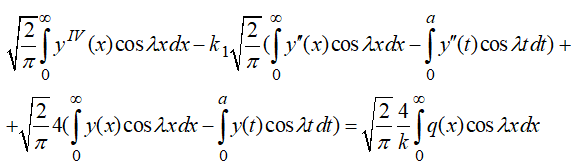(5)

Вводя соответствующие обозначения трансформант Фурье:

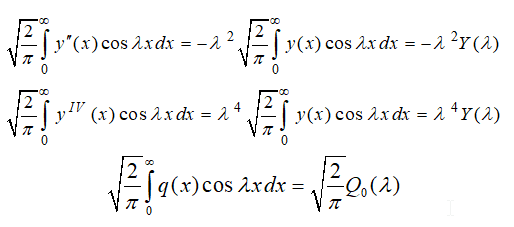	(5а)
	(5б)
	(5в)

Получим общий вид уравнения относительно новой координаты

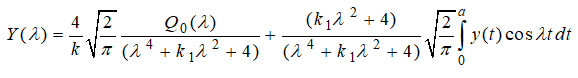(6)

Применяя к полученному выражению (6) обратное косинус преобразования Фурье получим искомую функцию прогиба.

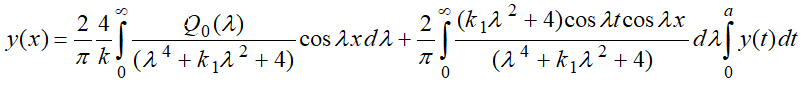(7)

Таким образом, применение к уравнению (3) прямого и обратного косинус преобразования Фурье позволяет свести дифференциальное уравнение (3) к интегральному уравнению относительно искомой функции прогиба балки у(x).

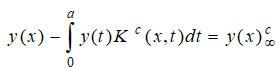(8)

В этом уравнении правая часть ˗  представляет собой прогиб бесконечной балки, загруженной заданной нагрузкой и полностью контактирующей с упругим двухпараметрическим основанием по всей длине.

Общий вид функции прогибов бесконечной балки для симметричных составляющих ˗  запишется в виде

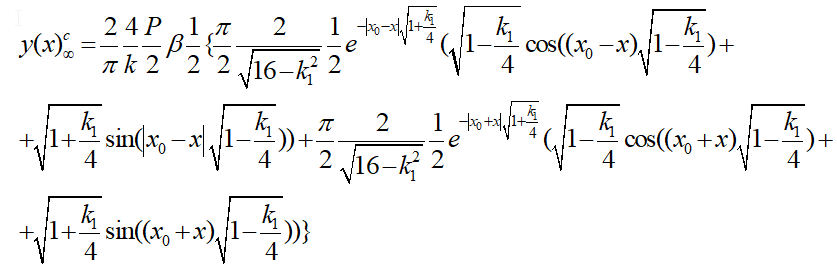(9)

Для частного случая, когда сосредоточенная нагрузка приложена в центре, т.е.  приведенное выражение примет вид

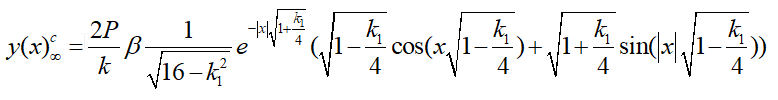(10)

Введем обозначения:

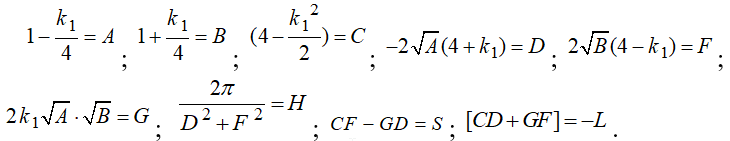(11)

Использование теории вычетов дает возможность выразить ядро интегрального уравнения (8)  через комбинацию тригонометрических и гиперболических функций

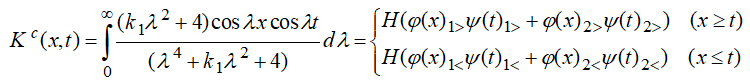(12)

где

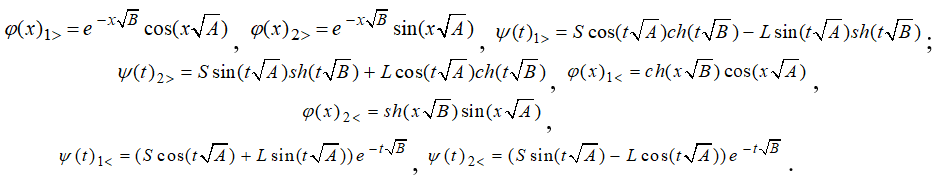(13)

Из выражения (12) следует, что ядро интегрального уравнения (8) –  вырожденное и что при его решении следует рассмотреть два случая. В первом из них предполагается, что точка, в которой ищется прогиб, находится в той части балки, где под ней есть основание. Очевидно, что в этом случае из (8) и (12) следует, выражение для определения функции прогиба балки

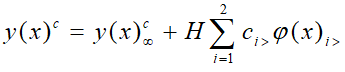(14)

здесь обозначено

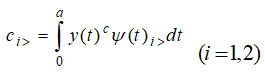(15)

Коэффициенты  могут быть определены в результате стандартной процедуры решения интегральных уравнений с вырожденным ядром. С этой целью обе части уравнения (14) умножаются последовательно на  и , а затем интегрируются от 0 до a.

Входящие в эти выражения функции  представляют собой интегралы от комбинаций функций  и , значения которых, могут быть выражены в явном виде.

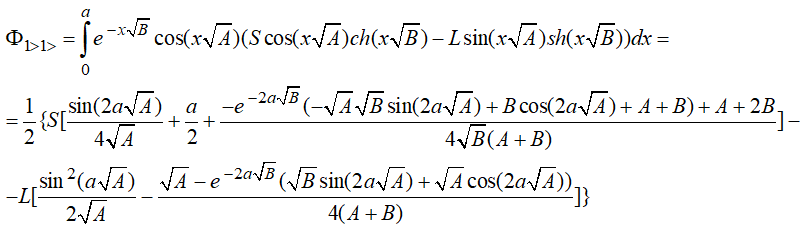
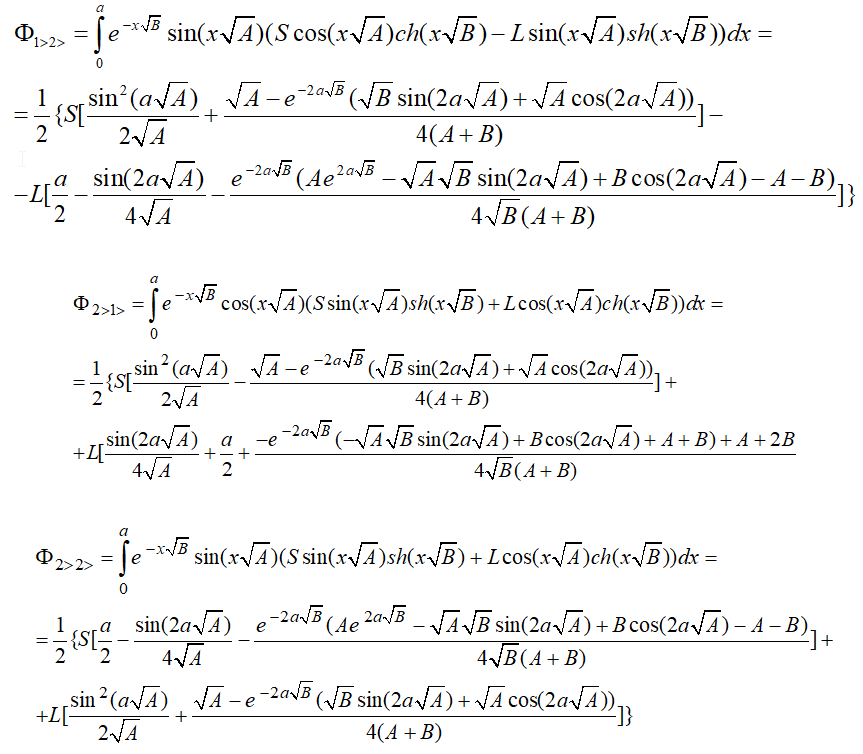
Для случая  с учетом (10) и (11) получим:

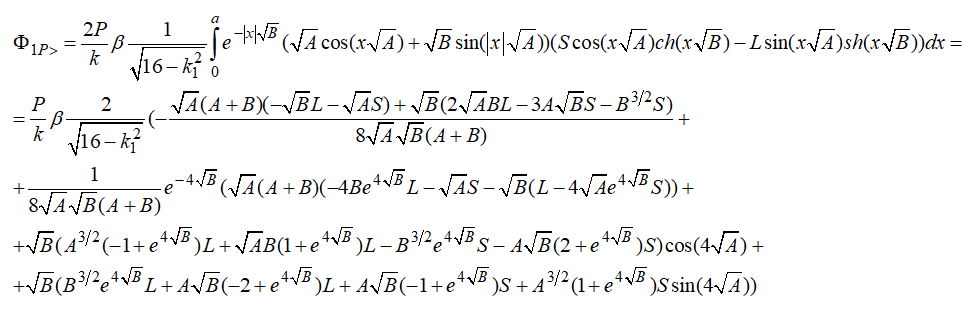
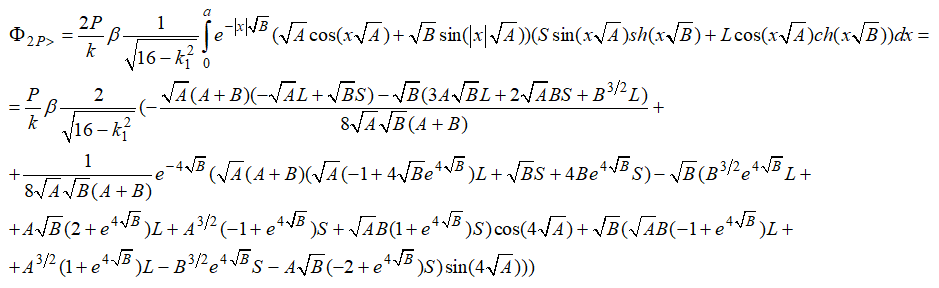
После определения коэффициентов  функция прогибов известна, следовательно известны и выражения углов поворота, изгибающих моментов и поперечных сил на рассматриваемом участке балки. Приведем их действительные значения для случая действия на балку сосредоточенной силы в центре

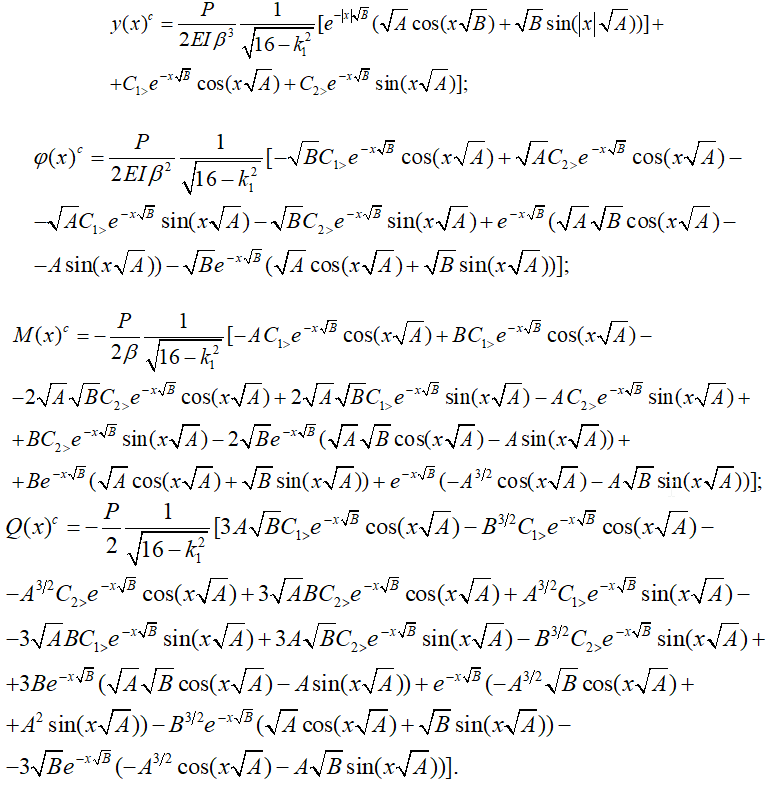(16)

Более сложно определить функцию прогиба на участке балки, где нет основания т.е. . В этом случае из (8) и (12) получим

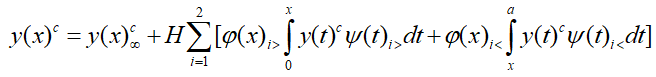(17)

Решение этого уравнения можно получить, например, методом последовательных приближений, причем соответствующие интегралы вычисляются в явном виде.

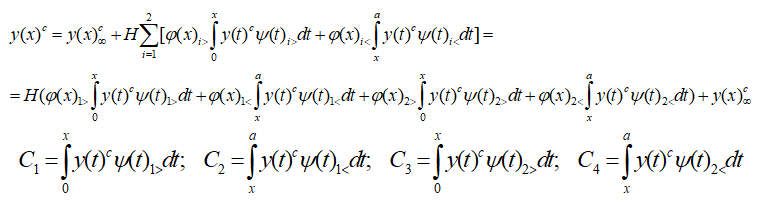	(18)
	(19)

 

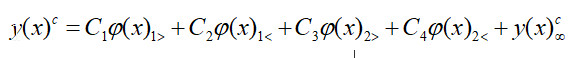(20)

Подставляем (20) в (19)

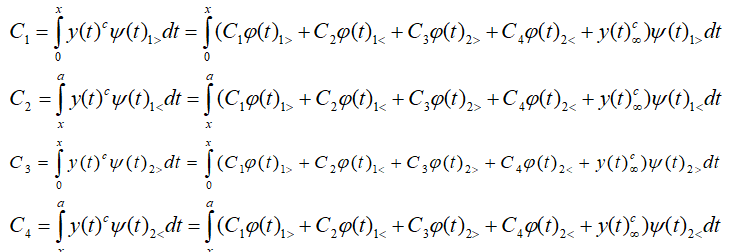
Приведем аналитический вид, вычисленных значений первых четырех интегралов представляющих собой соответствующие коэффициенты:

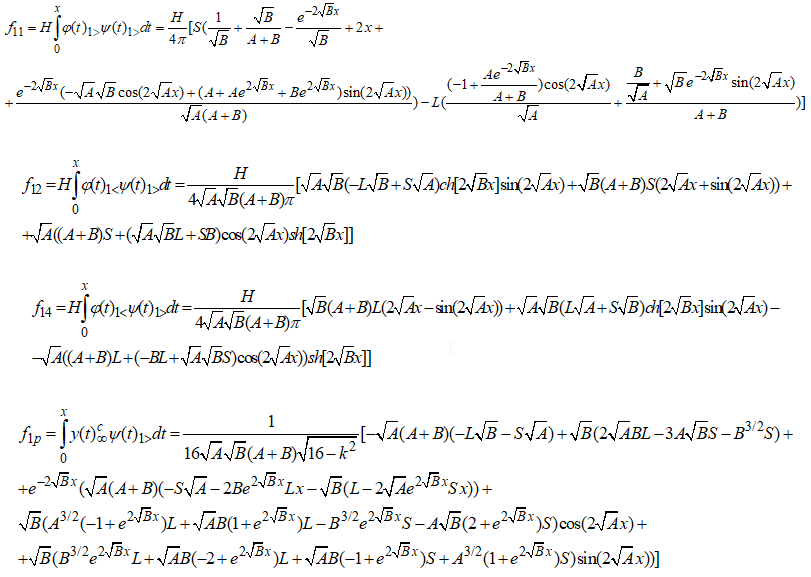
ОСНОВНОЙ РАЗДЕЛ

В качестве примера использования полученных зависимостей приведем расчет бесконечной балки, под центральной частью которой нет основания на приведенном расстоянии . Балка нагружена в центре сосредоточенной единичной силой. Эпюра приведенных прогибов показаны на рисунке 2 при различных значениях коэффициента сцепления.

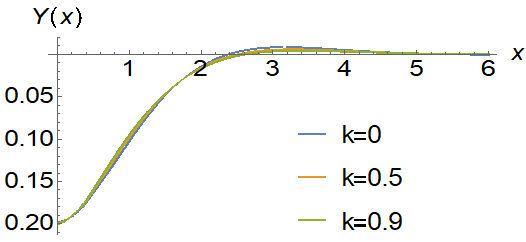
Рис.2. Прогиб бесконечной балки при величине провала основания  и ,, (разработано авторами).

При действии на балку кососимметричной нагрузки применяя синус – преобразование к дифференциальному уравнению (4) позволяет свести его к интегральному уравнению типа (12), но правой частью его будет функция прогиба бесконечной балки от заданной кососимметричной нагрузки , а ядром уравнения будет функция

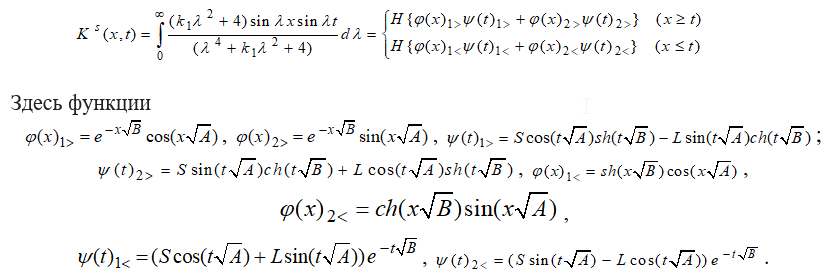(21)

ВЫВОДЫ

Совершенствование моделирования поведения бесконечной балки лежащей на основании, определяемом двумя обобщенными параметрами и имеющим провал под загруженной частью имеет важное значение для проектирования зданий и сооружений. Исследование может быть применено для анализа прочности и практического проектирования, например, ленточных фундаментов. Анализ результатов полученных при использовании различных значений коэффициентов показал, что предложенный метод расчета и рассматриваемая модель основания просты и удобны для практических расчетов и могут составить альтернативу другим инженерным методам. Предложенный метод расчета может быть просто и легко распространен на случаи, когда провал происходит не под одним, а под несколькими участками балки одновременно.

ЛИТЕРАТУРА

1. Власов, В.З. Балки, плиты и оболочки на упругом основании [Текст] / В.З. Власов, Н.Н. Леонтьев. — М.: Физматгиз, 1960. — 491с.
2. Пастернак, П.Л. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели [Текст] / П.Л. Пастернак. – М. – Л.: Госстройиздат, 1964. – 56 с.
3. Kerr, A.D. On the formal development of elastic foundation models. Ing.-Arc., 1984.
4. Колясина, С.А. Исследование влияния вариантов расчета грунтового основания и методов расчета коэффициентов постели на напряженно – деформированное состояние здания [Текст] / С.А. Колясина, П.И. Егоров. Электронное научное издание «Ученые заметки ТОГУ» 2014. — № 5 (2). — С. 21-34.
5. Vallabhan, C. V. G., Das, Y. C. An improved model for beams on elastic foundations / In Elastic-Plastic Failure Modelling of Structures with Applications Presented at the 1988.
6. Расчет конструкций на упругом основании [Текст] / М.И. Горбунов — Посадов, Т.А. Маликова, В.И. Соломин. – 3-е изд, перераб. и доп.– М.: Стройиздат, 1984. – 678 с.
7. Травуш, В.И., Александровский, М.В. Изгиб неизолированных прямоугольных плит, лежащих на двухпараметрическом основании [Текст] / В.И. Травуш, М.В. Александровский // Известия вузов. Строительство. — 1998. — №10. — С. 24-29.
8. Dinev, D. Analytical solution of beam on elastic foundation by singularity functions // Engineering Mechanics. — 2012. — Vol. 19. — № 6. – P. 381–392.
9. Травуш, В.И. Метод обобщенных решений в задачах изгиба плит на линейно-деформируемом основании [Текст] / В.И. Травуш // Строительная механика и расчет сооружений. — 1982. — № 1. — С. 24-28.
10. Wei, G.W. A new algorithm for solving some mechanical problems // Computer Methods in Applied Mechanics and Engineering, 190, 2017-2030, 2001.
11. Wei, G.W., Zhou, Y.C., Xiang, Y. Discrete singular convolution and its application to the analysis of plates with internal supports. Part 1: Theory and algorithm International Journal for Numerical Methods in Engineering, 55,913-946, 2002.
12. Травуш, В.И. Изгиб бесконечной балки на винклеровском упругом основании при отсутствии основания под частью балки [Текст] / В.И. Травуш, Фам Динь Ван // II Республиканская научно-техническая конференция. Научно технический прогресс и экология. — Актау. — 1992. – С. 70-76.
13. Маруфий, А.Т. Изгиб бесконечной балки на двухпараметрическом упругом основании с одним участком неполного контакта с основанием [Текст] / А.Т. Маруфий, Э.С. Рысбекова, А.А. Эгенбердиева // Вестник КГУСТА. — 2016. — №1. — С.252-256.